Algoritmos de ordenação
A ordenação é uma das operações mais efetuadas pelos computadores e tem como objetivo organizar uma lista de dados, facilitando a busca de determinada informação. A organização pode ser feita de forma crescente ou decrescente.
A complexidade de um algoritmo de ordenação varia conforme sua lógica de implementação, além disso, seu desempenho é afetado pelo tamanho do conjunto de dados a ser ordenado. Portanto, uma maneira de melhorar o desempenho na ordenação de grandes listas é utilizando mais núcleos do processador através a programação paralela.
Os algoritmos de ordenação podem ser divididos em dois grupos, aqueles que utilizam métodos simples de ordenação e os que utilizam métodos sofisticados de ordenação. Nos exemplos a seguir utilizei o algoritmo Merge sort, que faz parte do grupo que utiliza métodos sofisticados, aconselhado para ordenação de grandes listas de dados.
Biblioteca OpenMP
Uma forma de efetuar a programação paralela é utilizando a biblioteca OpenMP, compatível com a linguagem C++. Com esta biblioteca é possível dividir blocos do código para serem processados por diferentes threads, otimizando o processamento da ordenação. A divisão também é conhecida como working-sharing, que possibilita a separação de códigos de iterações (laços) ou de diferentes trechos do código (seção).
Para trabalhar com a premissa do working-sharing é necessário utilizar construtores específicos que definem o modo de execução dentro de uma região paralela. Existem 3 tipos destes construtores:
- #pragma omp for
- #pragma omp sections
- #pragma omp single
Para o exemplo utilizei a diretiva #pragma omp section, que permite a separação do código em seções, distribuindo cada parte entre o número de threads pré-definidas.
Merge Sort
O Merge Sort é um algoritmo de divisão e conquista com complexidade igual a n log n. Algoritmos desta classe efetuam a separação de uma lista de dados em duas partes, ordenam cada parte e as concatenam novamente, repetindo o processo até que a lista esteja totalmente ordenada.
No exemplo a seguir, a etapa de separação é feita por um processo recursivo, isto é, a lista é dividida em duas partes e a cada divisão o algoritmo chama a si mesmo novamente, enviando como parâmetro as novas sub listas. O processo é repetido até que não seja possível gerar uma nova dupla de sub listas.
Exemplo sem uso do OpenMP
void merge(char vIn[], int ini1, int fim1, int ini2, int fim2) {
int i, iSai;
int inicio = ini1;
for (iSai=ini1; iSai<=fim2; iSai++) {
if (ini1 > fim1) {
vOut[iSai] = vIn[ini2++];
} else if (ini2 > fim2) {
vOut[iSai] = vIn[ini1++];
} else if (vIn[ini1] < vIn[ini2]) {
vOut[iSai] = vIn[ini1++];
} else {
vOut[iSai] = vIn[ini2++];
}
}
for (i=inicio; i<=fim2; i++) {
vIn[i] = vOut[i];
}
}
void mergesort(char v[], int ini, int fim) {
int meio;
if (ini < fim) {
meio = (fim + ini) / 2;
mergesort(v, ini, meio);
mergesort(v, meio+1, fim);
merge(v, ini, meio, meio+1, fim);
}
}Exemplo com uso do OpenMP
void merge(char vIn[], int ini1, int fim1, int ini2, int fim2) {
int i, iSai;
int inicio = ini1;
for (iSai=ini1; iSai<=fim2; iSai++) {
if (ini1 > fim1) {
vOut[iSai] = vIn[ini2++];
} else if (ini2 > fim2) {
vOut[iSai] = vIn[ini1++];
} else if (vIn[ini1] < vIn[ini2]) {
vOut[iSai] = vIn[ini1++];
} else {
vOut[iSai] = vIn[ini2++];
}
}
for (i=inicio; i<=fim2; i++) {
vIn[i] = vOut[i];
}
}
void mergesort(char v[], int ini, int fim) {
int meio;
#pragma omp parallel shared(meio)
{
if (ini < fim) {
meio = (fim + ini) / 2;
#pragma omp sections
{
#pragma omp section
{
mergesort(v, ini, meio);
}
#pragma omp section
{
mergesort(v, meio+1, fim);
}
}
#pragma omp barrier
{
merge(v, ini, meio, meio+1, fim);
}
}
}
}Utilização de diretivas
Para implementar o Merge Sort de forma paralela, primeiro foi definida uma área paralela utilizando a diretiva #pragma omp parallel. Dessa forma, o código dentro da área paralela será executado pelas threads, que serão criadas conforme os núcleos disponíveis no processador ou alguma configuração de ambiente.
Ainda para essa diretiva, foi adicionado a opção shared, que permitirá compartilhar a variável int meio entre todas as threads.
Após isso, dentro da área definida como paralela, foi adicionado a diretiva #pragma omp sections, que define a área de código que terá conjuntos de seções independentes.
Dentro da área de seções, deve ser definido cada conjunto de seção. Portanto utiliza-se a diretiva #pragma omp section, separando cada bloco de código em seção. Dessa forma cada conjunto será compartilhado entre as threads.
No momento a parte paralela do código está finalizada, porém, ao tentar executá-lo, o resultado não será como o esperado, isto é, a lista ainda não estará ordenada. Isso acontece porque o array que contém nossa lista está sendo compartilhado entre as threads, porém temos uma parte do código que deve ser executada apenas quando toda a ordenação estiver pronta, caso contrário ocorre o que chamamos de condição de corrida.
Para resolver isso, após a área das seções foi utilizado a diretiva #pragma omp barrier, que define um ponto de sincronização entre todas as threads criadas, isto é, a área paralela aguarda a finalização de todas as threads antes de continuar.
Com essa última alteração nosso programa está pronto e funcionando como esperado.
Teste de Speedup
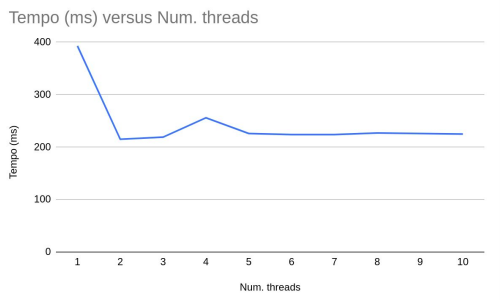
Para medir a performance do programa foram feitos alguns testes de speedup. Com este tipo de teste é possível medir o tempo total de processamento do programa em relação a quantidade de threads utilizadas.
Para 100.000 elementos os resultados foram os seguintes:
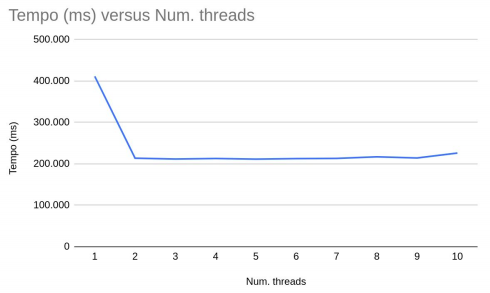
Para 100.000.000 elementos os resultados foram os seguintes:
Conclusão
Com os resultados obtidos podemos perceber uma melhora significativa com o uso de apenas duas threads, porém com o uso de 3 ou mais threads os resultados não tem grandes mudanças, isso porque começaram a surgir gargalos, ou seja, algumas threads ficam travadas esperando pelas outras, fazendo com que o tempo de execução não tenha diferença significativa.
Os testes foram executados em uma máquina com processador core i5 com 2 núcleos físicos e 4 processadores lógicos.